악곱 == 악성곱슬

0/1 배낭문제란?

다이나믹 프로그래밍 알고리즘을 이용해서 풀 수 있는 대표적인 유형의 문제이다.

가방에 적재할 수 있는 최대 무게가 주어지고, 여러 물건들이 주어진다. 여러 물건들은 각각 무게(weight)와 가치(value)를 갖게 되고, 어떤 조합으로 이 물건들을 가방에 적재해야 최대 “가치”를 갖게 할 수 있는가에 대한 문제이다.

물건의 가짓수가 적다면, 모든 조합의 경우의수를 다 구해보는 브루트 포스로 해결할 수도 있다. 하지만 이는 너무 막심한 손해다. 따라서 부분집합 중복 문제를 제거해주는 다이나믹 프로그래밍을 이용해서 어떻게 풀 수 있는지 알아보자.

위와 같은 조건이 있다고 해보자.

우선 2를 가방에 넣어본다. 그러면 2부터 7까지 모두 가방에 들어간 가치는 5가 될 것이다.

다음엔 6을 넣어본다.

최대치를 한번 보자.

• 기존에 2만 넣었을 때, 무게 7에서의 최대값 = 5
• 기존 1까지 무게를 채웠을 때 가치 + 6을 새롭게 넣어서 만든 가치 = 8

이 둘 간의 최대값을 구하면 된다. 즉, 가방에서 옛날 버전인 1까지의 최대값에 나를 더한 가치와 그냥 기존값 끼리 비교하여 더 큰 값을 선택하면 된다.

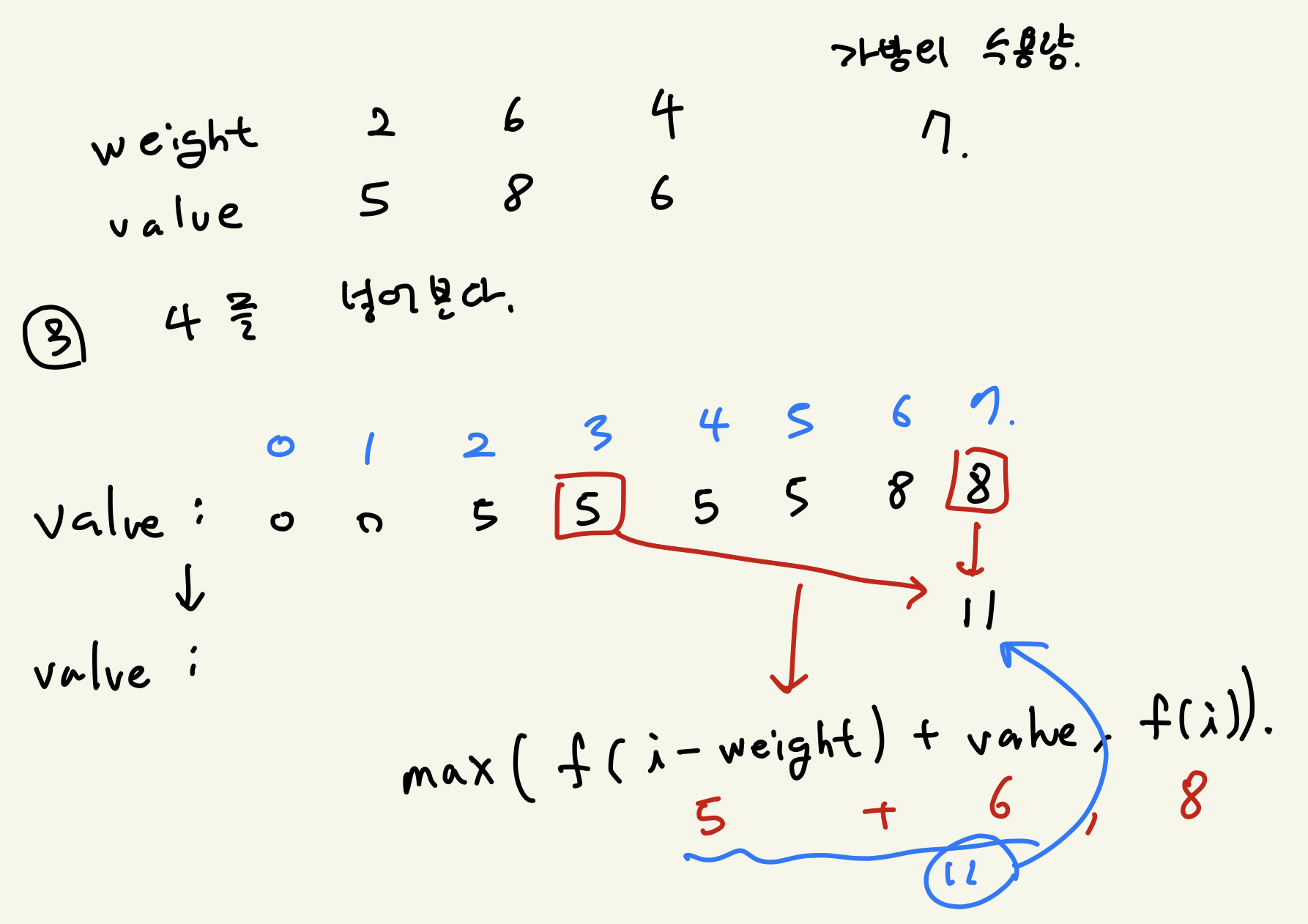
하나만 더해보자 4를 넣으면 다음과 같이 된다.

여기서는 2개를 비교하면 된다.

• 기존 2와 6을 넣어봤을때 무게 7까지의 최대값 = 8
• 기존 무게 3에서의 값 5 + 새로운 값 6 = 11

즉 이를 통해서 다음과 같은 점화식을 도출해 낼 수 있다.

f(i) = max( f(i - weight) + value, f(i))

위 식에서 중요한 점은 뒤에서부터 탐색을 해야 한다는 점이다. 왜냐하면 i - weight 때문에 앞에서부터 탐색을하게 되면 업데이트한 값으로 다시 비교를 하게 되서 “기존값” 이 사라지는 문제가 발생한다.

이와 비슷하지만, 물건을 쪼개서 넣을 수 있다면 fractional knapsack 문제로 그리디 알고리즘을 이용하여 풀 수 있다. 이럴 경우에는 그냥 무게당 가치가 가장 큰 값부터 다 넣으면 된다.

구현

---

# table: dp table (가방에 들어간 가치의 합)
# weightLimit: 가방의 한도
# knapsack: [weight, value] 형태의 튜플
def solution(weightLimit):
    table = [0] * (weightLimit+1)
    for w, v in knapsack:
        for i in range(maxKnapsack, w-1, -1):
            table[i] = max(table[i], table[i-w] + v)
    return table[-1]