[알고리즘] 플로이드 워셜(Floyd-Warshall)
플로이드 워셜 알고리즘이란?
플로이드 워셜 최단경로 알고리즘은 그래프에서 여러 노드가 있을 때, 모든 노드(All Source)에서 출발하여 다른 모든 노드(All Destination)로의 최단 경로를 구하는 알고리즘이다.
플로이드 알고리즘은 음수 사이클을 포함하면 사용할 수 없다는 특징을 갖는다. 다만 음수 사이클이 발생되지 않는한, 음수 간선은 포함할 수 있다.
음수 사이클이란 해당 경로를 무한 반복하면 음수 방향으로 계속 거리가 작아져서 수렴하지 않고 발산하는 경우를 말한다.
플로이드는 간단히 설명하면 I 로 부터 J 까지의 거리를 구하는데 K 라는 지점을 거쳐서 지나갈 때 최단경로가 나오는지 아닌지를 판별하며 Edge Relaxation을 통해 최단 거리를 업데이트 하는 알고리즘이다. Optimal substructure가 이곳에도 적용되는데, 최단 경로는 여러 개의 최단 경로로 이루어져 있다는 원리에 의해 음수 사이클이 발생할 수 없다는 전제가 설정된다. 이런 원리들에 의해 플로이드 알고리짐은 다이나믹 프로그래밍의 일종으로 분류한다.
어떻게 동작하는가?
플로이드 알고리즘의 동작 원리를 알아보자. A, B, C, D, E 5개의 노드중 A → D 라는 경로의 최단 경로를 구한다고 가정해보자.
플로이드 알고리즘에 의해 i 로 부터 j 까지의 거리를 구하는데 k 라는 지점을 거쳐서 지나가는 것이 빠른지, 아닌지를 판별한다. k는 A ~ E 까지 순회한다.

위 그림처럼, B → C 까지의 기존 경로와, B → A → C 의 경로중 어떤 값이 더 작은지를 판별해서 B → C 의 최단 거리를 업데이트 한다. 나머지 모든 노드들에 대해서도 동일하다. 참고로 자기 자신에 대해서는 모두 0으로 설정하기 때문에 A → A 같은 경우는 처리되지 않는다. B → A → A 같은 경우에도 A → A가 0이므로 B → A 와 동일하다.

k를 1 늘려서 같은 행동을 반복한다. 다만 여기서 A → E 를 보자. 이는 A → E 와 A → B → E 를 비교하게 되어있다. 그러나 B → E는 앞서 B → E 그 자체와 B → A → E 를 비교하여 최단 거리로 업데이트 한 값이다. 이를 통해 우리는 플로이드가 다이나믹 프로그래밍이라는 것을 알 수 있다. 즉 재귀적으로 메모이제이션을 사용하여 이전 값을 저장하거나, 바텀 업 방식으로 2차원 거리 테이블을 초기화 하여 업데이트 하는 방향으로 구현할 수 있음을 알 수 있다. 하나 더 보자.

마지막 k 가 E 까지 도달한 경우이다. 이 경우에도 결국엔 A → D, A → E, E→ D 모두 이미 이전(k-1)에 최적이라고 보장을 받은 값들이다. 따라서 A → D 와 A → E → D 를 비교하여 최종 결론을 내리고 더이상 업데이트할 요소가 없는 상태를 보장받을 수 있다. O(V^3)
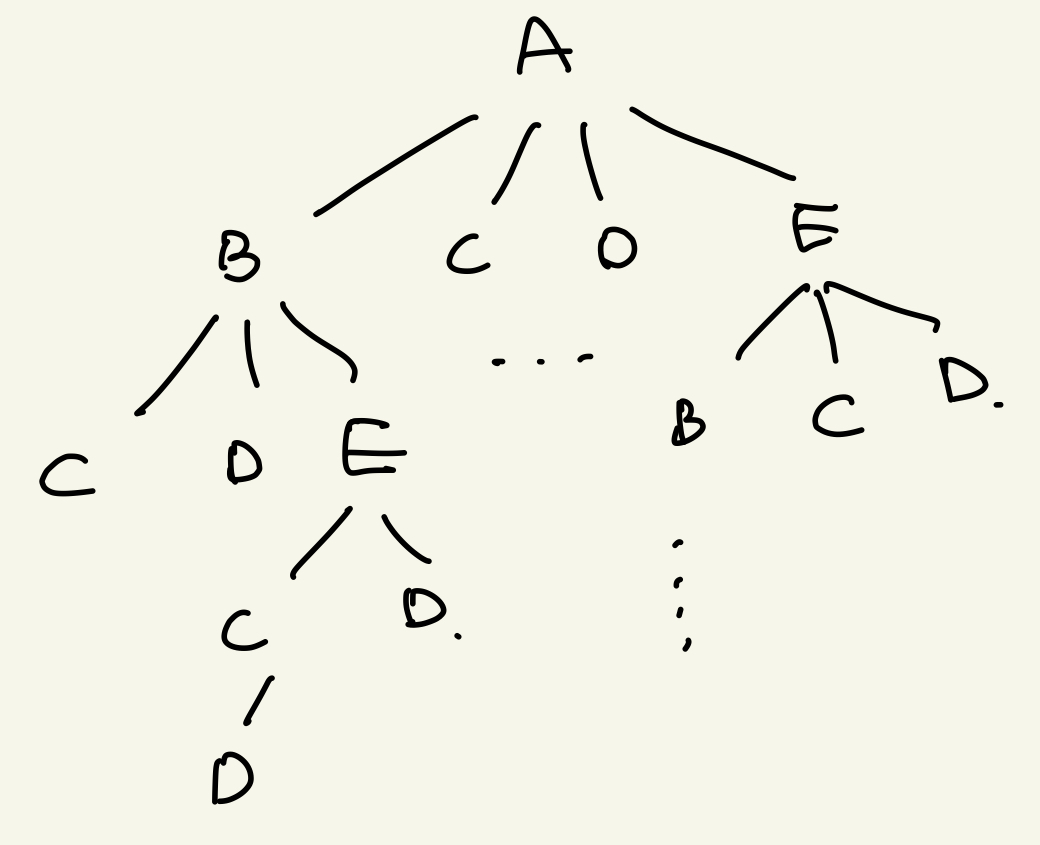
따라서 결국 위와 같은 트리 구조의 부분 문제를 미리 계산해놓는 다이나믹 프로그래밍으로 접근하여 풀 수 있는 문제라고 볼 수 있다.
구현(Python)
# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, v + 1):
for i in range(1, v + 1):
for j in range(1, v + 1):
# k를 지나치는 경로와, k를 지나치지 않는 경로중 더 짧은 경로로 업데이트
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
원리는 어렵지만 코드는 매우 간단하게 구현된다.