[알고리즘] LIS(Longest Incresing Subsequence) 최장 증가 부분수열
LIS란?
최장 증가 부분 수열을 의미한다.
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 “크다” 는 조건을 만족하고, 부분 집합의 크기가 가장 큰 경우를 최장 증가 부분 수열 이라고 한다.
자세한 내용은 아래와 같다.

주어진 수열에서 { (4 또는 2), 5, 8, 11, 15 } 를 고르게 되면 총 길이 5의 LIS가 나오게 된다. 다른 부분 수열들도 존재하지만 최장 길이를 갖는 부분수열은 위 5개를 고르는 경우이다.
구현 (Python) - O(N^2)
일반적으로 LIS를 구현하는 방법은 다이나믹 프로그래밍 알고리즘을 이용하는 것이다.
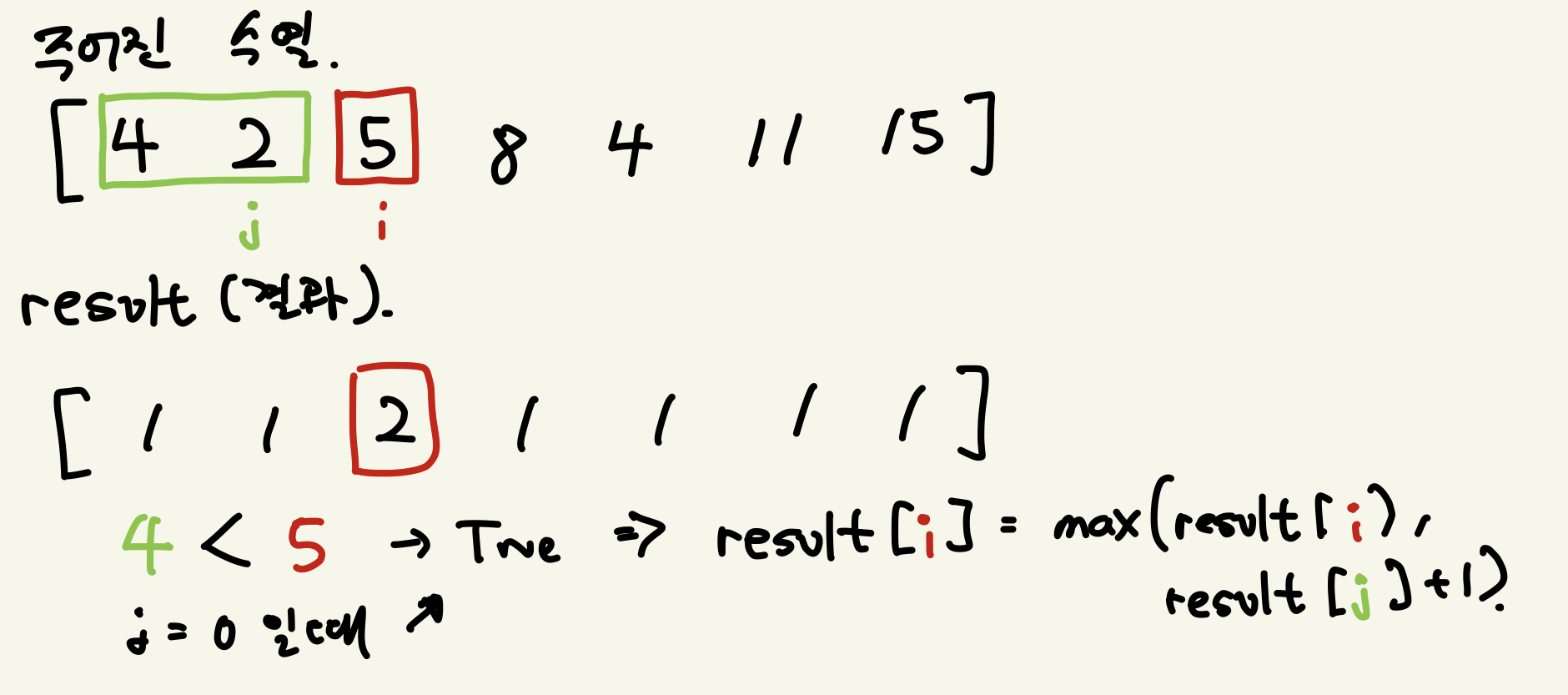
간단한 개념은 위와 같다.
- i 를 증가시키며 배열을 순차 탐색
- f(i) 와 f(j) 를 비교
- f(i)가 더 크다면 점화식 수행 → f(i) = max( f(i), f(j) + 1 )
2중 반복문을 사용하여 구할 수 있다. 코드는 다음과 같다. n은 전체 수열의 길이, 즉 전체 집합의 크기이다.
def lis(n):
result = [1] * n
for i in range(n):
for j in range(i):
if li[i] > li[j]: # 현재 값이 이전 값보다 클 경우
result[i] = max(result[i], result[j] + 1)
시간 복잡도 개선
앞서 알아본 LIS는 O(N^2) 알고리즘이다. 그러나 BOJ 12015 같이 인풋이 커지면 해당 알고리즘을 사용할 수 없다. 따라서 O(NlogN)으로 동작하는 LIS를 사용해야 한다. 이제 이를 알아보자.
해당 알고리즘을 통해서는 정확한 LIS 배열을 얻어낼 수 없다. 그냥 LIS의 크기만 알아낼 수 있다. 알고리즘은 다음과 같다.
- 빈 결과 리스트를 생성
- 주어진 수열을 순차 탐색하며 ( O(N) ) 아래 알고리즘대로 결과 리스트에 넣는다.
- 만약 결과 리스트에서 가장 오른쪽 값보다 크다면, 결과 리스트에 추가한다.
- 아니라면 결과 리스트에서 해당 값이 들어갈 수 있는 가장 왼쪽 인덱스를 찾아서 기존 값과 교체한다.
- 초기 배열 설정에 따라 결과를 반환한다.
이게 왜 되는가?
작을 때는 더 작은 값으로 업데이트 해봤자, 손해 볼 것이 없고, 결과 리스트는 계속 정렬이 된 상태로 운영되고, 맨 뒤에 제일 큰 값을 계속 추가하는 방향이므로 불필요한 탐색을 줄여 시간복잡도를 개선하는 방식이다. 다만 결과가 실제 LIS가 아니라는 점을 유의해야 한다. 10 20 30 40 1 2 3 의 경우 결과는 1 2 3 40 으로 도출될 것이다. 만약 1 2 3 뒤에 5 6 7 8 이 있었다고 한다면 미리 1 2 3을 안 넣어놓으면 LIS를 구할 수 없다. 그럼 만약 수열이 10 20 30 40 1 2 3 50 60 이라면? 더더욱 문제될 것이 없다.

구현 (Python) - O(NlogN)
빈 결과 리스트를 생성하지 않고 0을 하나 넣은 이유는, 이분 탐색시, 결과 리스트의 인덱스 에러를 방지하기 위함이다.
from bisect import bisect_left
def solution(seq): # seq는 주어진 수열(리스트)이다.
result = [0]
for s in seq:
if result[-1] < s:
result.append(s)
else:
result[bisect_left(result, s)] = s
return len(result) - 1