악곱 == 악성곱슬

위상정렬, DP

---

이 문제는 게임에서 건물을 짓는 순서가 주어지고, 어떤 특정 건물을 지을 때 까지의 시간을 출력하는 문제이다. 건물을 짓는 순서는 단방향 그래프와 같다.

이 문제에서 건물의 순서가 주어지고, 그래프임을 보았을 때 위상정렬임을 깨달을 수 있다. 다만 한 가지 특이한 점은 더 오래 걸리는 건물에 의해 다음 건물의 소요시간이 결정된다는 점이다. 따라서 여기서 DP를 이용해서 문제를 추가적으로 해결할 수 있다.

1. in degree가 0인 노드들을 시작노드로 설정, queue에 삽입
2. 하나씩 queue에서 pop → cur_node
   1. 만약 타겟 노드(건물 W)라면 break
3. cur_node의 인접 노드(to_node)들을 검사
   1. f(to_node) = max(f(to_node), f(cur_node) + time(to_node)
   2. 인접 노드의 in degree를 하나 뺀다.
   3. 만약 인접 노드의 in degree가 0이라면 queue에 삽입

3-a 의 점화식은 다음과 같은 상황을 뜻한다.

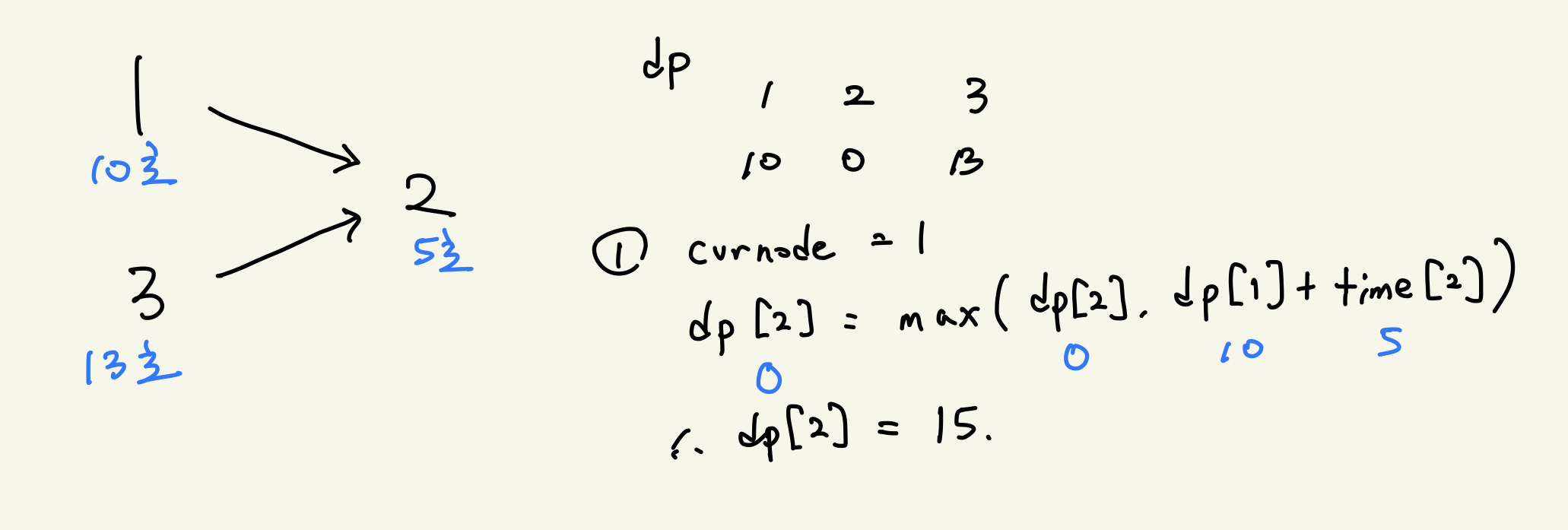
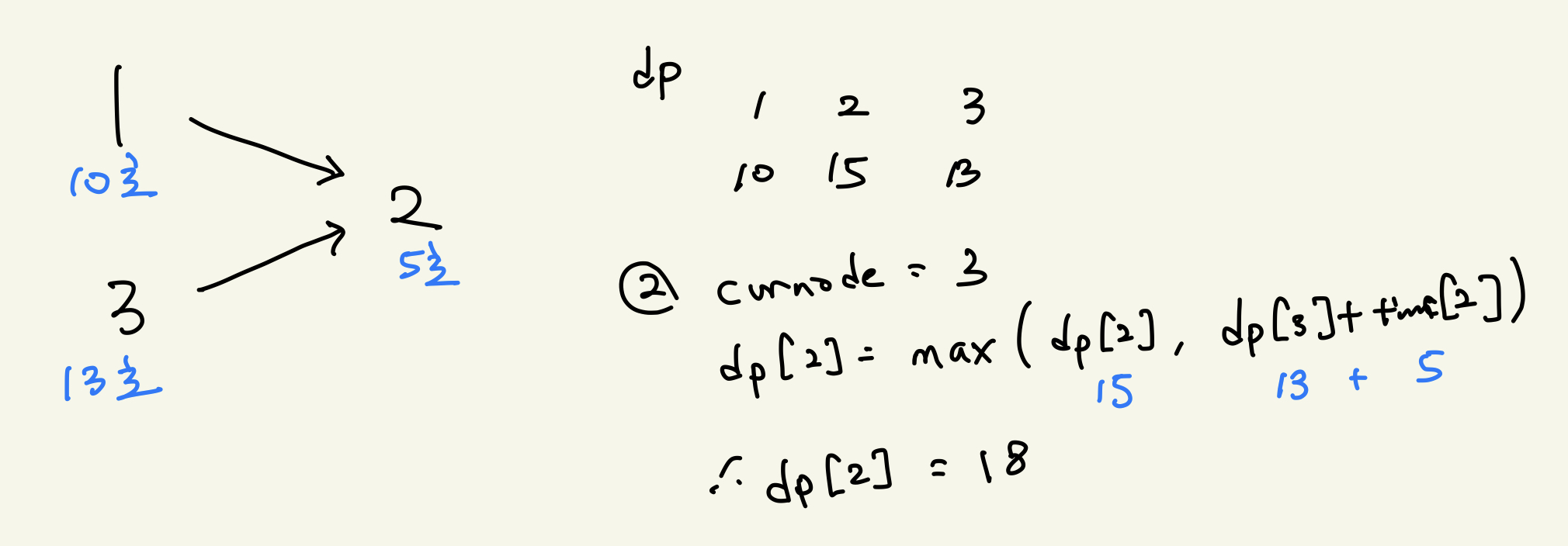
구현

---

import sys
from collections import deque

def solution(target_w, n):
    que = deque()
    dp = [0] * (n + 1)
    # in degree 가 0인 노드를 start node로 설정
    for i in range(1, n+1):
        if not in_degree[i]:
            que.append(i)
            dp[i] = time[i]

    while que:
        cur_node = que.popleft()
        if cur_node == target_w:
            break
        for to_node in graph[cur_node]:
            # dp를 사용해서 더 오래걸리는 건물(경로)로 계속 업데이트
            dp[to_node] = max(dp[to_node], (dp[cur_node] + time[to_node]))
            in_degree[to_node] -= 1
            # in degree 가 0 인 노드를 queue 에 삽입
            if not in_degree[to_node]:
                que.append(to_node)
    return dp[target_w]

if __name__ == "__main__":
    T = int(sys.stdin.readline().rstrip())
    for _ in range(T):
        N, K = map(int, sys.stdin.readline().rstrip().split())
        time = [0] + list(map(int, sys.stdin.readline().rstrip().split()))
        in_degree = [0] * (N + 1)
        graph = [[] for _ in range(N + 1)]
        for _ in range(K):
            X, Y = map(int, sys.stdin.readline().rstrip().split())
            graph[X].append(Y)
            in_degree[Y] += 1
        W = int(sys.stdin.readline().rstrip())
        print(solution(W, N))