악곱 == 악성곱슬

DP

---

행렬 [N, M] x [M, K] 에 대한 곱셈 연산의 수는 N x M x K 이다.

여러개의 행렬이 쭉 있을때 뭐 부터 곱해야 행렬 곱셈 연산의 수가 최소가 될지 구하는 문제이다.

아래 사진과 같은 행렬이 주어졌다고 생각해보자.

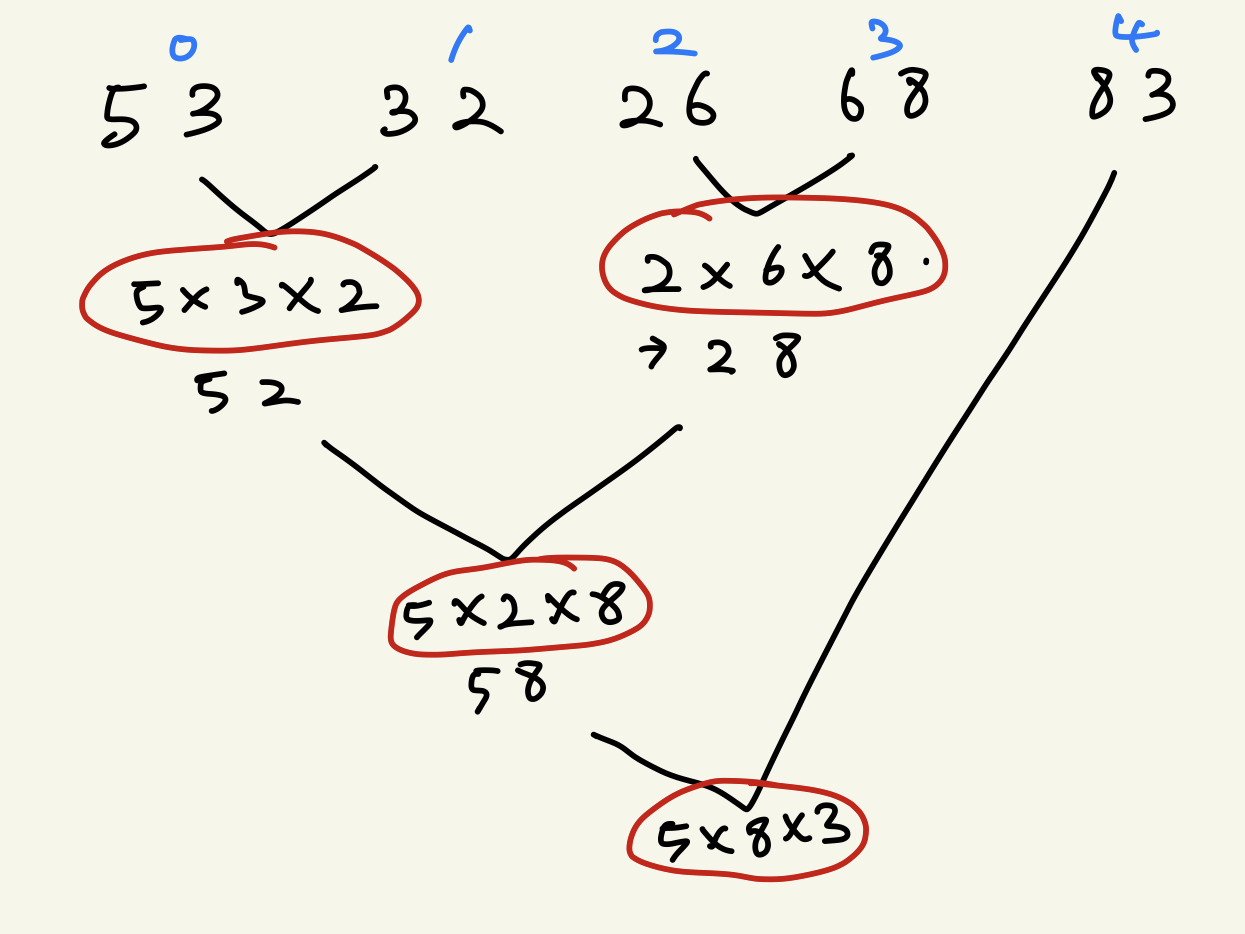
위 사진이 최소 값이라는 것은 아니고 문제를 푸는 방식에 대한 이해를 해본 것이다. 자세히 들여다 보면 행렬에 대한 모든게 필요한 것이 아니라 row, col 에 대한 숫자 정보가 순서를 해치지 않고 연산이 되면 되는 것이다.

따라서 위 행렬 정보를 리스트 하나로 관리 하면 된다.

• [ 5, 3, 2, 6, 8, 3 ]

이제 이를 통해서 어떻게 곱 연산 수의 최소값을 찾을 수 있을지 알아보자.

해당 문제를 풀기 위해 구해야 할 것은 0~len(list) 까지의 곱을 어떻게 최소화 할 것인가를 구해야 하므로 이를 f(0, N-1) 로 설정한다. 그렇게 되면 풀어야 할 문제는 아래 사진과 같다.

하위 sub problem에서 어떻게 잘라서 곱했을 때 최소값이 나왔는지를 이미 알고있다고 가정한다면 위 식을 구할 수 있다. 따라서 DFS, 재귀적으로 위 트리를 순회하며 메모이제이션을 활용하면 해결할 수 있다.

위 사진의 점화식에 오류가 있어서 식을 다시 쓰면 아래와 같다 (i 가 아니라 mid임)

• f(row, col) = min( { mid = row + 1 ~ col - 1} | f(row, mid) + f(mid, col) + (list[row] x list[mid] x list[col])

이를 코드로 구현하면 다음과 같다.

구현

---

함정이 하나 있었다. 행렬이 1개일 때도 만족해야 한다. 따라서 예외처리를 해주었다.

import sys

def matrix_size_mul(num1, num2, num3):
    return num1 * num2 * num3

# Top-Down DP
def dp(row, col):
    if col - row < 2:
        return 0
    if col - row == 2:
        return matrix_size_mul(numbers[row], numbers[row+1], numbers[row+2])    # row + 2 == col

    mem[row][col] = INF
    for mid in range(row+1, col):
        if not mem[row][mid]:
            mem[row][mid] = dp(row, mid)
        if not mem[mid][col]:
            mem[mid][col] = dp(mid, col)

        mem[row][col] = min(
            mem[row][col],
            mem[row][mid] + mem[mid][col] + matrix_size_mul(numbers[row], numbers[mid], numbers[col])
        )

    return mem[row][col]

if __name__ == "__main__":
    INF = int(1e9)
    N = int(sys.stdin.readline().rstrip())
    # 매트릭스 숫자 받는 부분
    numbers = []
    r, c = map(int, sys.stdin.readline().rstrip().split())
    if N == 1:
        print(r * c)
    else:
        numbers.append(r)
        numbers.append(c)
        for _ in range(N-1):
            r, c = map(int, sys.stdin.readline().rstrip().split())
            numbers.append(c)

        # TOP-DOWN DP
        mem = [[0]*len(numbers) for _ in range(len(numbers))]
        print(dp(0, len(numbers)-1))