[자료구조] 해시테이블
해싱(Hashing)
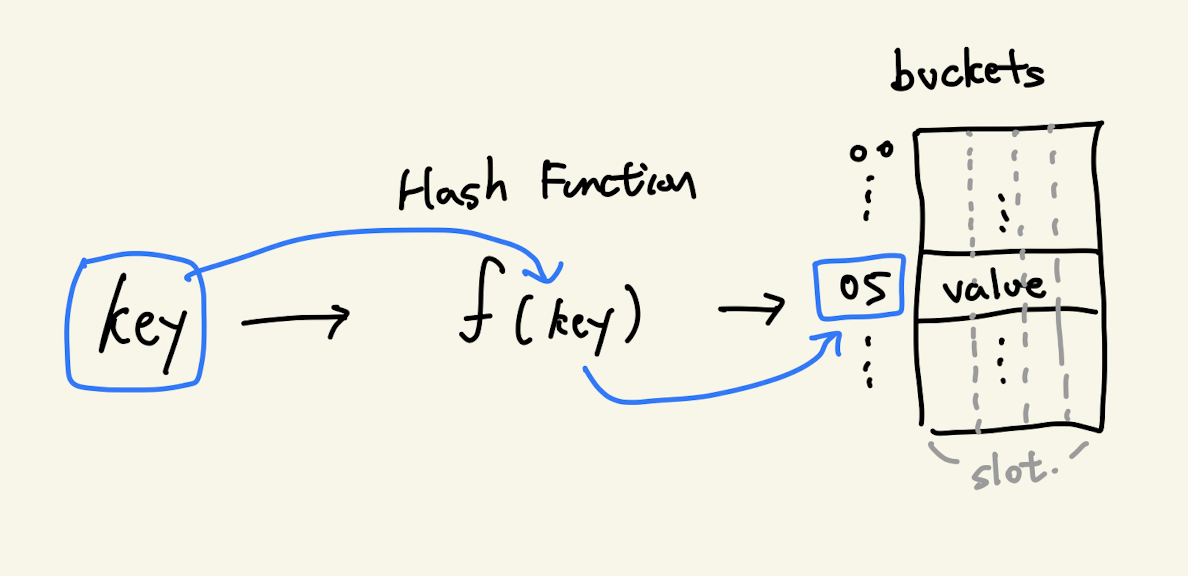
해싱은 키(key)값을 해시함수(Hash Function)에 대입하여 얻은 결과를 주소로 사용하여 순차탐색하지 않고 바로 값에 접근할 수 있게 하는 기법이다. 따라서 O(1)의 시간복잡도에 탐색이 가능하다.
사용하는 자료구조에 따라 여러 방법으로 다음과 같이 나눌 수 있다.
- 정적 해싱(해시 테이블)
- 동적 해싱(이진트리, 트라이)
- 확장 해싱(디렉터리 + 해시테이블)
정적 해싱
정적 해싱이란, 고정 크기 배열을 이용한 방법. 고정 크기 배열이란 해시테이블을 말한다.
- 슬롯: 한 개 의 데이터를 저장할 수 있는 공간.
- 버킷: 동일한 주소(인덱스)를 갖는 데이터 저장 공간. 동일 한 주소의 버킷에 여러 슬롯이 있을 수 있는 것.
- 해시 테이블: 한개 이상의 버킷들로 구성
- 해시 함수: 키를 주소로 변환하는 함수
장점
- 상수 시간(O(1))에 탐색, 저장, 삭제가 가능하다. 즉, 빠르다
단점
- 버킷의 크기를 작게 설정하면 충돌의 우려가 있고, 너무 크게 잡으면 메모리 낭비의 우려가 있다.
충돌(collision) & 버킷 오버플로우(overflow)
- 충돌: hash_function(key)의 값보다 hash_table의 크기가 더 작아서 다른 key임에도 인덱스 값이 중복되는 경우를 말한다.
- 버킷 오버플로우: 버킷의 slot이 가득차서 더이상 저장할 수 없는 상태를 말한다. 즉, 충돌이 slot의 크기보다 많이 발생한 경우이다.
충돌과 버킷 오버플로우를 다루는 방법 2가지
- 해시 함수의 결과값이 최대한 균등(uniform)하게 나올 수 있도록 한다.
- 체이닝과 개방주소법 등을 통한 충돌과 오버플로우가 발생했을때 처리해준다.
체이닝
- 오버플로우가 발생한 버킷뒤로 링크드리스트를 구현하는 것.
- 장점
- 오버플로우가 발생한 곳만 뒤로 연결해주면 됨
- 단점
- 충돌이 많이 발생할수록 링크드리스트 연결 요소가 많아지고, 성능이 나빠진다.
- 성능의 척도는 한 버킷당 연결된 데이터의 평균 개수가 된다. 최악의 경우 한개의 버킷에 모든 데이터가 연결될 수 있으므로(단일 링크드리스트) O(n)의 탐색 시간복잡도를 갖게 될 수도 있다.
개방 주소법
- 오버플로우가 발생하면 다른 주소에 넣겠다는 의미로 개방 주소법이다. 여러가지 방법이 있다.
- 선형 탐색(linear probing): 충돌시 n칸 뒤의 버킷에 데이터 삽입. n은 고정크기. n칸씩 고정적으로 움직이기 때문에 선형임.
- 선형 탐색은 Primary clustering에 취약하다는 단점이 있다.
- primary clustering이란, 다른 모든 버킷이 차있어서 빈 칸을 찾을 때까지 오랜 시간이 걸리는 문제.
- 제곱 탐색(quadratic probing): 충돌시 n칸 뒤의 버킷에 데이터 삽입. 다만 n은 제곱수. 1^2 → 2^2 → 3^2…
- 제곱 탐색은 Second clustering에 취약하다는 단점이 있다.
- second clustering이란, 초기 해시값이 같다면, 다음에 탐색되는 지점이 전부 갖다는 문제점.
- 이중 해시(double hashing): 2개의 해시 함수를 이용하여 하나는 최초의 해시값, 둘째는 충돌이 일어났을때 이동할 칸 수를 구해주는 용도로 사용한다.
- 이중 해시를 사용하면 선형, 제곱의 단점을 보완할 수 있다. 최초 해시값이 갖다면 이동 폭이 두번째 해시 함수에 의해 달라지기 때문에.