악곱 == 악성곱슬

힙(heap) 구조

---

힙은 최댓값(max-heap), 최솟값(min-heap)을 빠르게 구하기 위해 고안된 완전이진트리(complete binary tree)형태의 자료구조이다.

트리구조이므로 데이터를 추가하는 비용은 O(logN)이다.

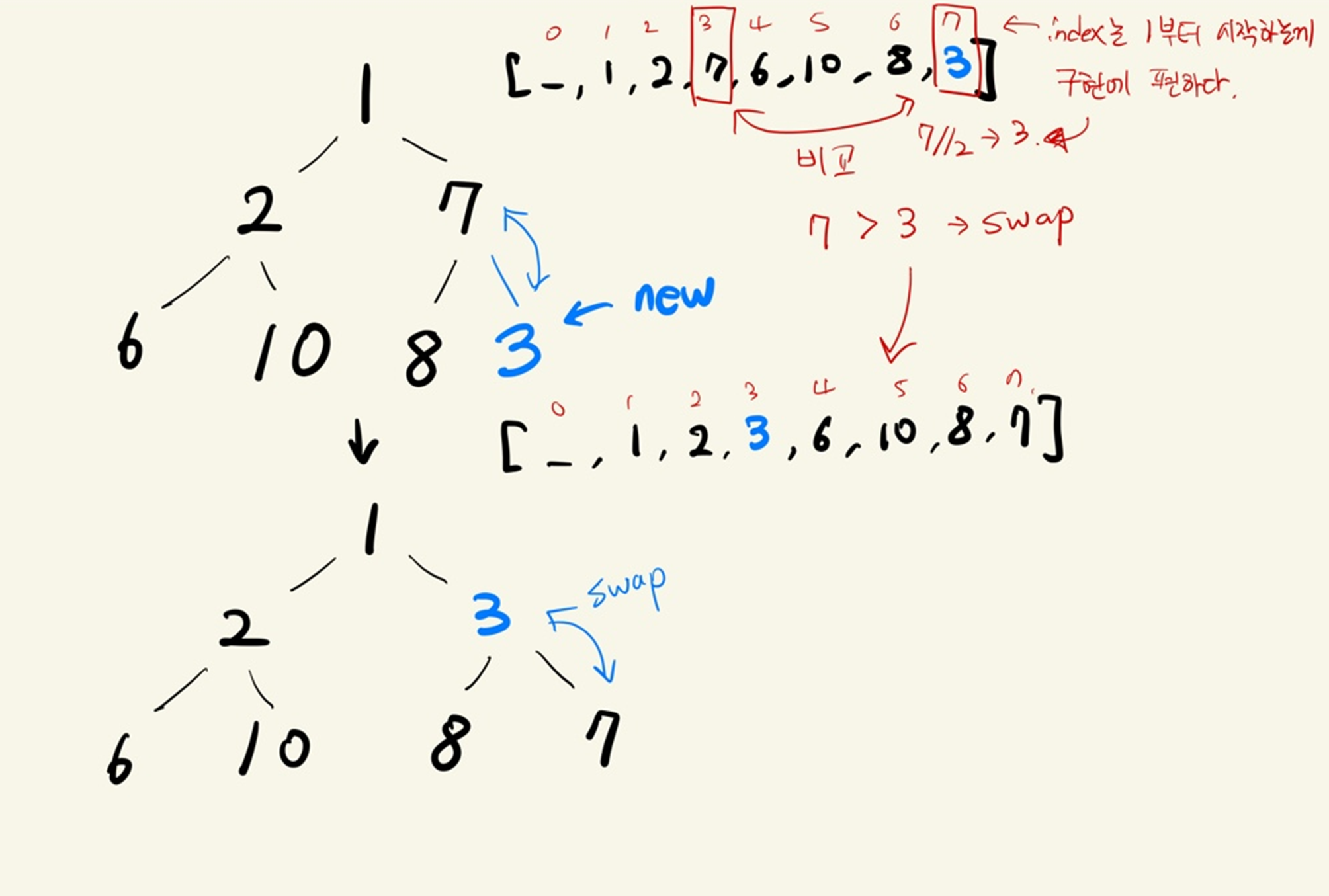
위 그림에서 배열의 인덱스를 1부터 시작하도록 표시했는데 그렇게 해야 child // 2 == parent가 성립하기 때문이다. 0으로 해도 상관없다, 그에 맞춰 구현하기만 한다면

데이터를 추출하는 비용은 O(logN)이다. 추출하는 비용은 우선순위가 가장 높은 데이터, 즉 트리의 root 원소를 pop하면 되기 때문에 1 같지만, pop 후에는 가장 마지막 원소를 제일 위(root)로 올린 후 제 자리로 찾아가는 과정이 포함되므로 O(logN)이다.

힙 구조에서 명심해야 할 것은 root원소는 가장 높/낮은 것은 맞지만 그 이후 노드들의 정렬은 꼭 순서대로가 아니라는 점이다. 위 그림만 봐도 10과 8,7의 인덱스 순서가 순서대로가 아니다. 단순히 parent와 child사이의 대소비교만 할 뿐이다.

파이썬에서의 힙 구조(heapq)

---

import heapq

heapq 모듈은 이진 트리(binary tree)기반의 최소 힙(min-heap) 자료구조를 제공한다.

heap = []  # heapq에서 사용할 빈 리스트 생성

heapq는 리스트를 힙 처럼 다룰 수 있도록 도와주는 모듈이므로 빈 리스트를 위와 같이 생성해야 한다.

heapq.heappush(heap, <원소>)  # <원소> 자리에 원하는 데이터 추가
heapq.heappush(heap, (key, "value"))

위 코드와 같이 데이터를 추가한다. → O(logN)

데이터에는 우선순위가 있어야 한다. 따라서 {키, 이름} 같은 데이터에서 키를 기준으로 정렬하고 싶다면 키를 key로 추가할 수 있다.

root = heapq.heappop(heap)  # root 원소 제거 및 반환

루트 원소 제거 및 반환 → O(logN)

heapq.heapify(heap)  # list를 heap으로 변환

heapify() 함수에 리스트를 인자로 넘기면 해당 리스트가 heap 구조에 맞게 재배치 된다.

max-heap으로 변환하고 싶다면 heappush에서 부호를 변환하면 된다. 추출할 때는 다시 부호를 변환해서 가져오면 된다.

힙 정렬(heapsort)

리스트를 heap 구조에 넣었다가(heappush) 하나씩 빼면서(heappop) 정렬할 수 있다. → O(NlogN)

우선순위 큐

---

우선순위 큐는 큐와 스택과 비슷한 축약 자료형이다. 다만 각 원소들이 우선순위를 갖고 있다.

우선순위 큐 힙과 다르다. 우선순위 큐는 “리스트”, “맵”과 같은 추상적인 개념이다. 마치, “리스트”를 연결리스트(Linked List)나 배열로 구현할 수 있는 것과 같은 개념이다.

우선순위 큐는 두 가지 기능을 포함해야 한다.

• 원소를 우선순위를 지정해서 삽입
• 가장 우선순위가 높은 원소의 제거

우선순위 큐는 여러 방식으로 구현할 수 있다.

• 배열, 연결리스트, heap구조 → 배열과 연결리스트의 경우에는 효율이 좋지 못하여 보통 트리 기반의 heap구조를 이용하여 구현한다.