악곱 == 악성곱슬

DP

---

항상 문제를 풀다보면 sub problem의 중복 문제를 찾고 그것을 해소하기 위해 dp table이나 메모이제이션을 사용하는 방향으로 DP 생각이 나서 풀게 된다. 그래서 어찌 보면 DFS랑 되게 유사하게 생각의 사고를 시작하게 되는 것 같다.

이 문제는 2, 3, 5만 소인수로 갖는 N 번째 숫자를 반복해서 찾아야 하는 문제이다. 딱봐도 중복 문제가 엄청 나오게 생겼다. 그래서 DP를 고려하기 시작했다.

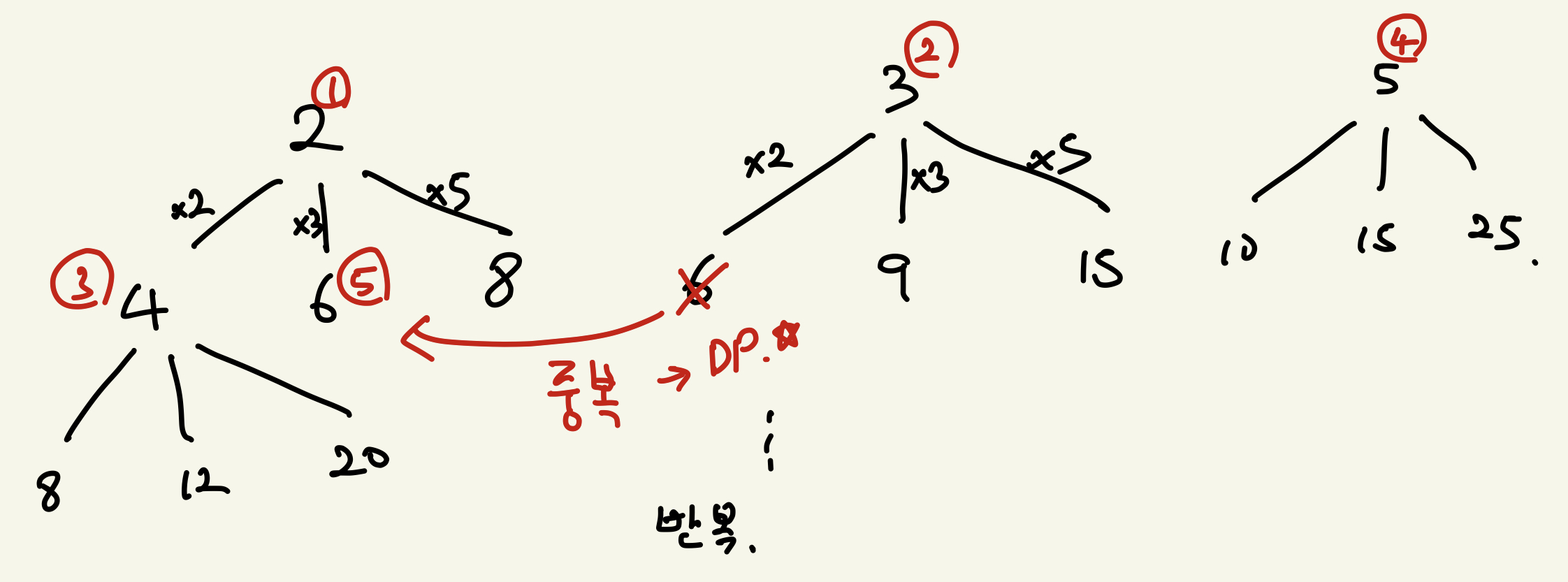
이런식으로 중복 문제가 발생하고 이를 메모이제이션 해야 시간복잡도를 줄일 수 있음을 알 수 있다.

다만 여기서는 해당 숫자가 등장했는지만 알아보면 되므로, set 자료구조를 사용하여 skip 하는 식으로 구현하면 된다.

그리고, N 번쨰 오름차순으로 하나씩 세어줘야 하므로 min-heap을 사용해서 가장 최소값을 계속 pop할 수 있도록 구현한다.

1. 초기에 1은 넣어놓고, 2, 3, 5를 min-heap, set 자료구조에 넣는다.
2. 하나 pop 해서 결과 리스트에 넣고, x2, x3, x5 한 값을 min-heap, set 자료구조에 넣는다.
   1. 만약 x2, x3, x5한 값이 set 자료구조에 있다면 min-heap에는 넣지 않는다.
3. 최대 1500번 째 수를 반환해야 하므로 10억까지 반복한다.
4. 입력이 주어지는대로 미리 계산한 결과 리스트에서 값을 하나씩 출력한다.

코드는 다음과 같다.

구현

---

import sys
import heapq

def solution(m):
    calc = [2, 3, 5]
    heap = []
    for c in calc:
        heapq.heappush(heap, c)
        c_set.add(c)
    cur = 0
    while cur <= m:
        cur = heapq.heappop(heap)
        cache.append(cur)
        for dc in calc:
            if cur * dc in c_set:
                continue
            heapq.heappush(heap, cur * dc)
            c_set.add(cur * dc)

if __name__ == "__main__":
    cache = [1]
    c_set = {1}
    MAX = int(1e9)
    solution(MAX)
    while True:
        N = int(sys.stdin.readline().rstrip())
        if N == 0:
            break
        print(cache[N-1])  # N번째 못생긴 수