[이코테] 5. 정렬
관련 코드 구현
개념
정렬이란 데이터를 특정한 기준에 따라서 순서대로 나열하는 것이다. 정렬알고리즘으로 데이터를 정렬하면 다음 장에서 배울 이진 탐색(Binary Search)가 가능해진다. 정렬 알고리즘은 이진 탐색의 전처리 과정이기도 하니 빠삭하게 알아야 한다.
정렬 알고리즘은 종류가 매우 다양하다. 선택 정렬(Selection Sort), 삽입 정렬(Insertion Sort), 퀵 정렬(Quick Sort), 계수 정렬(Counting Sort)등이 있다.
일반적으로, 문제에서 요구하는 조건에 따라 적절한 정렬 알고리즘이 공식처럼 사용된다. 상황에 맞지 않는 알고리즘을 사용한다면 프로그램은 비효율적으로 동작한다.
아래 각 알고리즘은 모두 오름차순을 기준으로 설명한다.
선택 정렬(Selection Sort)
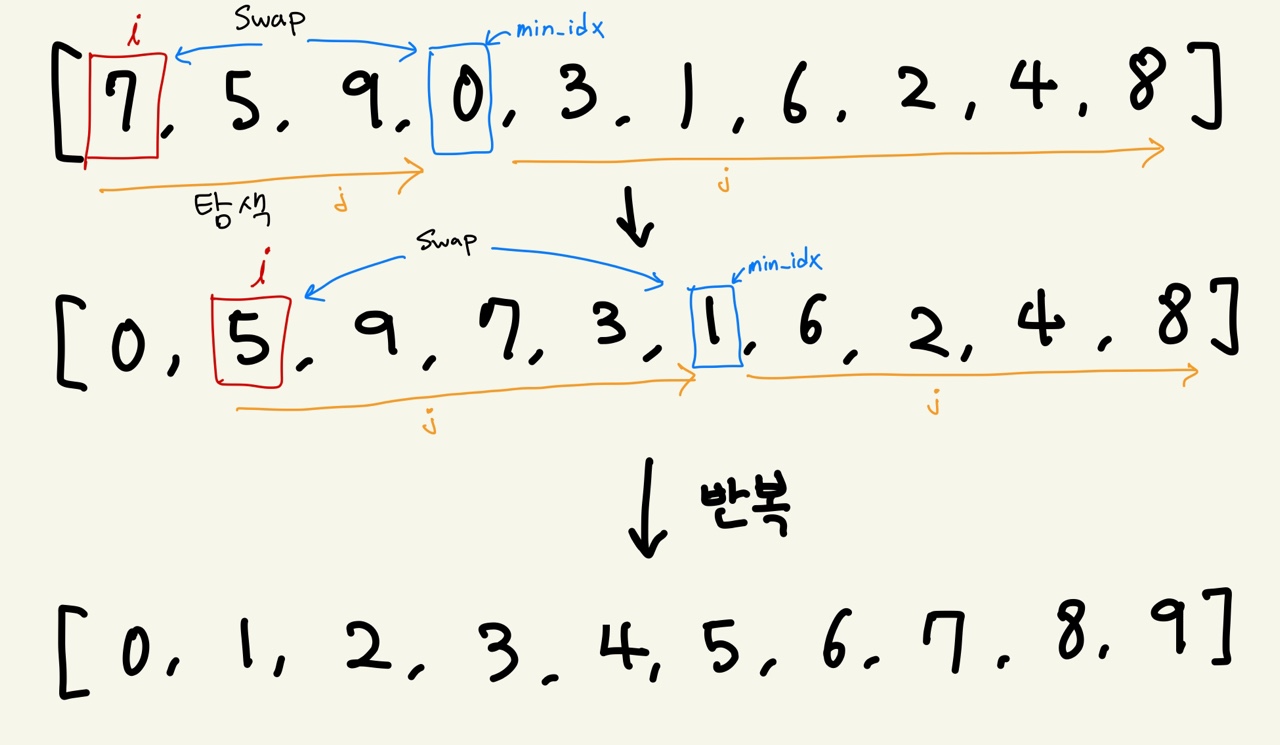
가장 작은 데이터를 선택해서 맨 앞에 있는 데이터와 바꾸고, 그 다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정의 반복
즉, 원시적으로 가장 작은것을 선택해서 교체한다는 의미로 선택정렬 이라고 한다.
# 오름차순 정렬 selection sort
def selection_sort(li): # 파라미터로 1차원 리스트
li_len = len(li) # 리스트의 길이
for i in range(li_len):
min_idx = i # 가장 왼쪽 인덱스 저장
for j in range(i+1, li_len): # 가장 작은 원소의 인덱스 탐색
if li[min_idx] > li[j]: # 탐색하며 업데이트
min_idx = j
# 가장 작은 원소와 스왑
li[i], li[min_idx] = li[min_idx], li[i]
return li
print(selection_sort([7, 5, 9, 0, 3, 1, 6, 2, 4, 8]))
선택 정렬은 N-1번 만큼 가장 작은 수를 찾아서 맨 앞으로 보내야 한다. 위 2중 for문에 대해 근사치를 구해보면 N x (N + 1) / 2 번의 연산을 수행한다. 이는 O(N^2) 이다.
선택 정렬 자체는 정렬 알고리즘들에 비교했을때 매우 비효율적인 성능을 갖는다. 하지만 특정 리스트에서 가장 작은 데이터를 찾는 일이 코딩 테스트에서 잦으므로 위의 형태에 익숙해질 필요가 있다.
삽입 정렬(Insertion Sort)
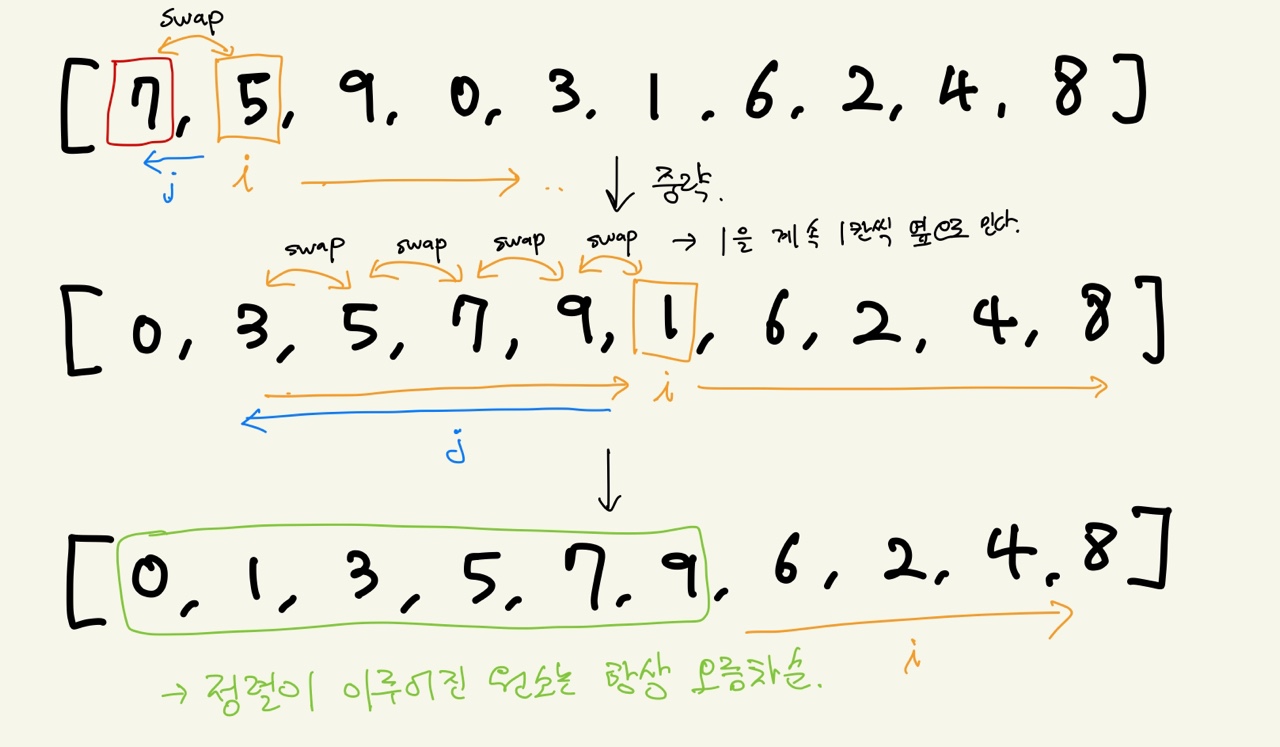
데이터를 하나씩 확인하며, 각 데이터를 적절한 위치에 삽입한다.
삽입 정렬은 선택 정렬에 비해 구현 난이도가 높지만 시간 측면에서 더 효율적이다. 삽입정렬은 필요할 때만 위치를 바꾸므로 데이터가 거의 정렬 되어 있을 때 매우 효율적이다.
삽입 정렬은 특정한 데이터를 적절한 위치에 삽입한다는 의미에서 붙은 이름이다. 또한, 삽입 정렬은 특정한 데이터가 적절한 위치에 들어가기 이전에, 그 앞까지의 데이터는 이미 정렬되어 있다고 가정한다.
삽입 정렬은 두 번째 데이터부터 시작한다. 첫 데이터는 그 자체로 정렬되어 있다고 판단하기 때문이다.
# insertion sort 오름차순
def insertion_sort(li):
li_len = len(li) # 1차원 리스트 길이
for i in range(1, li_len):
for j in range(i, 0, -1): # 현재위치부터 왼쪽으로 이동하며 탐색
if li[j] < li[j-1]: # 한칸씩 왼쪽으로 이동
li[j], li[j - 1] = li[j - 1], li[j] # 이동을 swap 으로 구현
else: # 자신보다 작은 데이터를 만나면 그 위치에서 멈춤
break
print(insertion_sort([7, 5, 9, 0, 3, 1, 6, 2, 4, 8]))
삽입 정렬의 시간복잡도 또한 O(N^2)이다. 선택정렬과 마찬가지로 2중 for문이 사용된 것을 볼 수 있다. 하지만 앞서 말한 내용과 같이 거의 정렬이 되어있는 상황(Best Case)에서는 훨씬 빠르게 동작한다는 점이다. 완벽히 정렬되어 있는 리스트의 경우 O(N)으로 수행속도가 짧아지며 뒤에 배울 O(NlogN)알고리즘들 보다 빠르게 동작한다는 점이다.
따라서 문제에 따라 입력이 거의 정렬되어 있는 상태로 주어진다면 삽입 정렬을 이용하는 것이 정답 확률을 높일 수 있다.
퀵 정렬(Quick Sort)
기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾼다.
퀵 정렬은 기준을 설정한 다음 큰 수와 작은 수를 교환한 후 리스트를 반으로 나누는 방식으로 동작한다.
퀵 정렬에서는 피벗(pivot)이 사용된다. 큰 숫자와 작은 숫자를 교환할 때, 교환하기 위한 ‘기준’을 피벗이라 한다. 피벗을 설정하여 리스트를 분할하는 방법에 따라 여러 방식으로 퀵 정렬을 구분하는데 호어 분할(Hoare Partition) 방식을 기준으로 설명한다.
- 리스트에서 첫 번째 데이터를 피벗으로 정한다.
피벗을 설정 후 왼쪽에서 피벗보다 큰 데이터를 찾고, 오른쪽에서부터 피벗보다 작은 데이터를 찾는다. 그리고 서로 위치를 교환해준다.
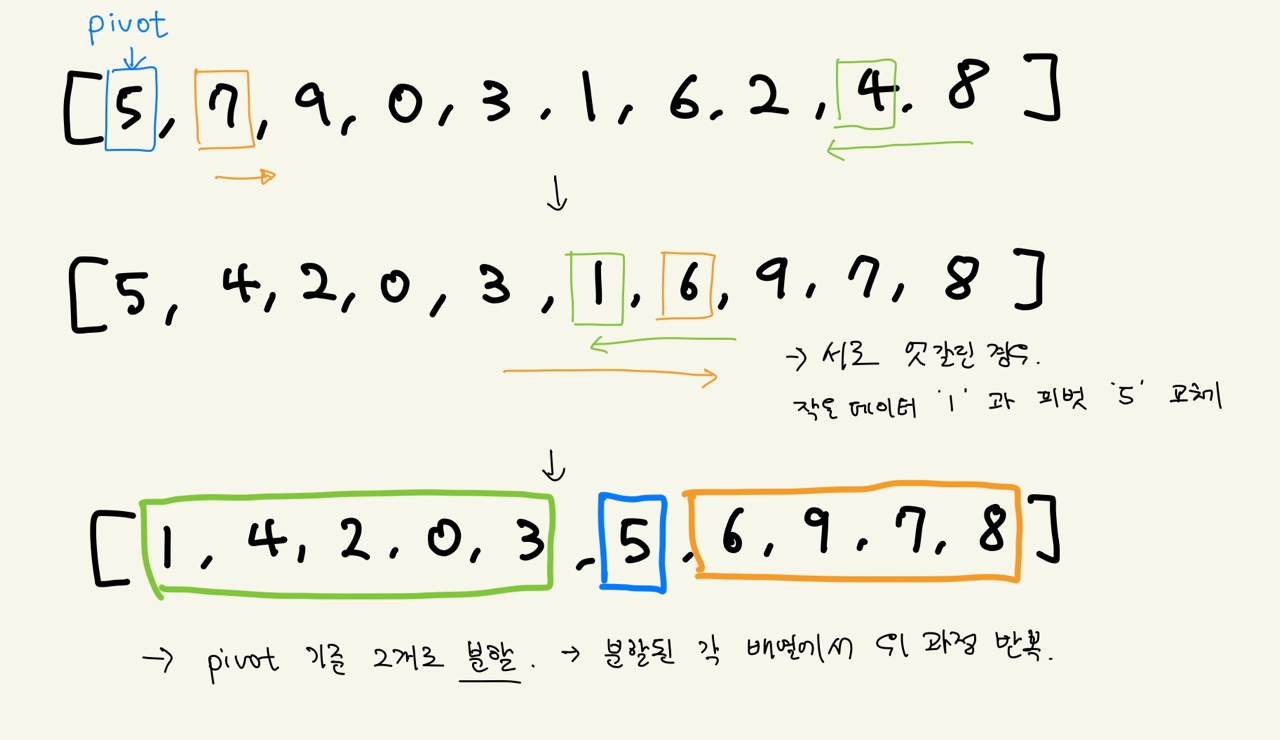
가운데 그림과 같이 서로 엇갈린 경우 작은 데이터를 pivot과 교체해준다.
피벗이 이동한 상태에서 왼쪽과 오른쪽의 리스트는 피벗을 기준으로 작은 것들끼리, 큰 것들끼리 모이게 된다. 이렇게 위치하도록 하는 작업을 분할(Divide) 혹은 파티션(Partition)이라고 한다.
위 과정을 각 리스트 마다 재귀적으로 반복하면 아래와 같이 정렬이 이루어진다.
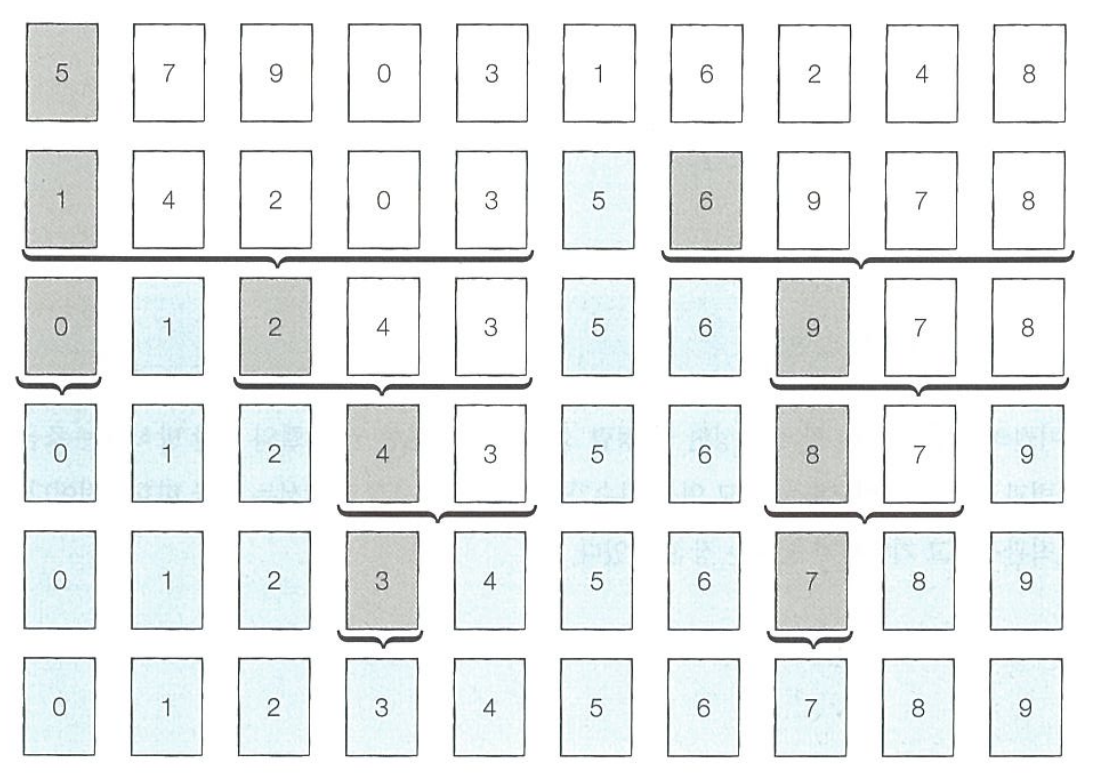
아래는 정석 quick_sort의 코드이다.
# 리턴이 없는 버전
def quick_sort(li, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start # 피벗은 첫 번째 원소
left = start + 1
right = end
while left <= right:
# 피벗보다 큰 데이터를 찾을 때까지 반복
while left <= end and li[left] <= li[pivot]:
left += 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while right > start and li[right] >= li[pivot]:
right -= 1
# 엇갈렸다면 피벗과 교체
if left > right:
li[right], li[pivot] = li[pivot], li[right]
# 정상적인 상황이라면 left, right 교체
else:
li[left], li[right] = li[right], li[left]
# 분할 이후 왼쪽 리스트, 오른쪽 리스트 각각 재귀
quick_sort(li, start, right - 1)
quick_sort(li, right + 1, end)
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
quick_sort(array, 0, len(array) - 1)
print(array)
아래는 파이썬의 장점을 살린 quick_sort 코드이다
# 리턴이 있는 버전
def quick_sort(li):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(li) <= 1:
return li
pivot = li[0] # 피벗 == 첫 번째 원소
tail = li[1:] # 피벗을 제외한 나머지
left_side = [x for x in tail if x <= pivot] # 분할된 왼쪽 부분
right_side = [x for x in tail if x > pivot] # 분할된 오른쪽 부분
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행, 전체 리스트 반환
# + 연산을 통해 리스트 병합
# 왼쪽, 오른쪽의 리스트를 각각 재귀적으로 연산
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
print(quick_sort(array))
퀵 정렬의 평균 시간복잡도는 NlogN이다.
위 코드처럼 가장 왼쪽의 데이터를 pivot으로 삼을 경우 정렬이 완벽히 되어 있는 경우 문제가 발생한다. 리스트를 절반씩 분할하는 것이 최적인데 그렇게 하지 못하고 10개의 데이터를 1, 9 → 1, 1, 8 → 1, 1, 1, 7 → … 이런식으로 이어나가서 NlogN을 보장하지 못하고 O(N^2)이 되어버리는 것이다.
따라서 데이터가 무작위로 입력되는 경우 위 코드의 알고리즘이 빠르게 동작할 확률이 높다.
randomized quick sort: 위 문제점을 보완하기 위해 피벗을 랜덤하게 추출해주는 방식이다.
계수 정렬(Count Sort)
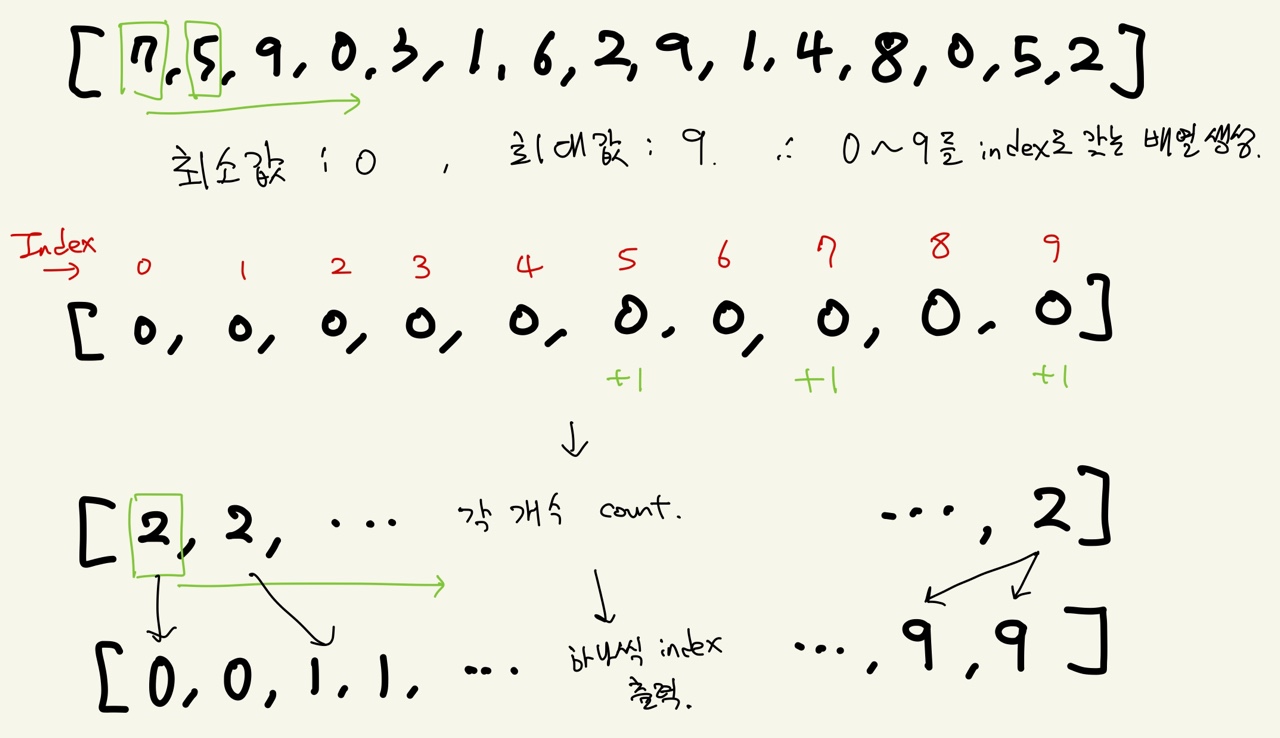
데이터의 개수를 저장하고 낮은 인덱스부터 세어주며 반환하는 원리
계수 정렬은 특정한 조건이 부합할 때만 사용할 수 있다.
- 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때, 주로 가장 작은 데이터와 큰 데이터의 차이가 1,000,000을 넘지 않을 때 효과적이다.
- 데이터의 범위만큼 미리 리스트를 만들어놔야 하는데 범위가 너무 크면 메모리 초과, 시간초과 등 여러 문제가 발생할 수 있다.
- ex): 0~100점 사이의 성적 데이터 (정수)
데이터 개수를 N, 데이터의 최대값을 K라고 할 때 시간복잡도는 O(N + K)이다.
계수 정렬의 공간 복잡도는 상황에 따라서 심각한 비효율성을 초래할 수 있다. 데이터가 단 2개인데 0과 999,999인 경우에도 리스트의 크기는 100만이 되어야 한다. 따라서 데이터의 특성을 완전히 파악할 수 있는 경우에 적절히 사용하면 좋다.
def count_sort(li):
# 모든 범위를 포함하는 리스트 선언 (0으로 초기화)
count = [0] * (max(li) + 1)
result = list()
# 데이터에 해당하는 인덱스의 값 증가
for num in li:
count[num] += 1
# 리스트에 기록된 정렬 정보를 통해 새로운 result 에 정렬
for i in range(len(count)):
for j in range(count[i]):
result.append(i)
return result
array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
print(count_sort(array))
파이썬의 정렬 라이브러리
파이썬 기본 정렬 라이브러리는 항상 최악의 경우에도 시간복잡도 O(NlogN)을 보장한다.
- sort, sorted
array = [('바나나', 2), ('사과', 5), ('당근', 3)]
def setting(data):
return data[1]
result = sorted(array, key=setting)
print(result)
array = [('바나나', 2), ('사과', 5), ('당근', 3)]
array.sort(key=lambda x: x[1])
print(array)
위 두 코드는 같은 결과를 반환한다.